I write here because I like writing. Simple as that. Some of it is technical, some of it is just thoughts and little ideas. No tracking, no engagement farming or ads – just words on a page.

Things you might be looking for

• Blog posts – Browse the latest or check out posts by topic
• Code & Projects – My GitHub or Git server
• Self-hosted services – If you're a friend or family member looking for something, you probably already know where to go. If not, ask me directly.
• Contact – Reach out to me on Matrix

Who I am

I like open source, decentralized tech, and figuring things out for myself. I love D&D, public transport and Europe. I would've liked to use the term cyberpunk to describe my blog, hadn't it already been used to describe a dystopian hyper-capitalist setting.

Hashtags

Use any of these hashtags to find posts about that topic!

#bayesian #doomsdayargument #foss #functional #korea #languagedesign #maths #philosophy #politics #publictransport #regulation #segmentdisplay #traffic

Recent is de Vomar begonnen met koopzegels zoals de Albert Heijn dat ook heeft. Ze adverteren met 6% rente, maar ik heb een manier gevonden hoe je 100% rente van ze terug kunt krijgen. Ook laat ik zien waarom koopzegels zelden de moeite waard zijn om te sparen.

Wat zijn koopzegels?

Koopzegels bestaan bij de Albert Heijn al 70 jaar: sinds 1955 kun je koopzegels kopen bij de Albert Heijn.

Voor elke euro aan boodschappen kun je één koopzegel van 10 cent kopen. Heb je een boekje vol van 490 koopzegels, dan krijg je daar 52 euro voor terug. Zo investeer je €49,– in de AH koopzegels, en krijg je vervolgens 6% rente daarop terug!

“Als je geld spaart in Nederland, dan is de kans groot dat de bank je minder dan 2% rente geeft. Maar er is een manier om 6% rente te verdienen, gegarandeerd en zonder risico's.” (vertaald uit het Engels) Zo schrijft Mew op hun blog “My Expat Wallet”. Ook andere blogs gericht op geld besparen lijken lovend over de koopzegels. “Met de huidige lage rentetarieven is het sparen van koopzegels echter interessanter geworden,” schrijft Martijn in de blog op onlinegeldverdienen.nl.

Hoe werken de kooppunten van de Vomar?

De kooppunten van de Vomar zijn tien keer zo klein: in plaats van een koopzegel van 10 cent per euro boodschappen, krijg je bij de Vomar een kooppunt van 1 cent per 10 cent boodschappen.

Wat me echter het meest opviel, was dat je je punten altijd kunt verzilveren, wanneer je maar wilt. Je hoeft dus niet te wachten totdat je 4900 kooppunten hebt opgespaard om dan precies €52,– uitgekeerd te krijgen. Zodra je je geld komt ophalen bij de servicebalie, krijg je het geld en de 6% rente mee, ongeacht het totaalbedrag.

Ook viel het me op dat ze hun rente altijd naar boven afronden. Als je een kooppunt van 1 cent koopt bij de Vomar en die meteen verzilvert, dan ronden ze af en dan verdien je 2 cent! Dat is een renteverdubbeling van 100% die je meteen na de kassa mag komen ophalen bij de servicebalie! Blijf een middag je geld verdubbelen, en je bent binnen de kortste tijd miljonair.

Ik had het heel leuk gevonden om nu een foto te laten zien van een gigantische villa die ik gekocht zou hebben door m'n geld te verdubbelen met koopzegels van de Vomar, maar ik moet je helaas teleurstellen: zo gratis is dit niet. Je koopt de koopzegels naast je boodschappen, dus in het beste geval koop je 10 cent aan boodschappen plus 1 cent voor een koopzegel, en daarvoor krijg je 2 cent terug. Netto gezien betaal je dus 9 cent per keer. Met andere woorden: de 100% rente levert je uiteindelijk maar 10% korting op je boodschappen.

Hoe kan dit?

De misleidende truc ligt in het feit dat je niet 6% rente krijgt op je boodschappen, maar 6% rente op 10% van de prijs. Koopzegels zijn een belabberde vorm van 0,6% korting krijgen op al je boodschappen. Koopzegels klinken alleen maar beter omdat ze je 6% laten vergelijken met hoeveel rente je spaarrekening oplevert.

Ook misleiden ze je met het idee dat je vollédige spaarrekening ineens 6% rente zou krijgen. Voordat de Albert Heijn je 6% rente geeft op je spaarrekening, moet je tien keer je volledige spaarrekening uitbetalen aan de Albert Heijn!

Gesimuleerd voorbeeld

Volgens het Nibud heeft een gezin van twee ouders en twee kinderen minimaal €20,83 per dag nodig aan eten. Hierbij rekent het Nibud geen andere kosten mee die je maakt bij de supermarkt, zoals bijvoorbeeld toiletpapier, schoonmaakmiddelen of shampoo, maar laten we uitgaan van een dagelijkse uitgave bij de Albert Heijn van €30,–.

Het gezin is aan het budgetteren, en ze willen wat spaargeld verzamelen en besluiten mee te doen aan koopzegels. Ze kopen 30 koopzegels per dag, en proberen de boekjes zo vaak mogelijk te verzilveren. Hoeveel denk je dat ze aan het einde van het jaar bij elkaar hebben gespaard?

In deze grafiek heb ik vier strategieën meegenomen:

1. Het gezin doet mee aan koopzegels. Als ze hun spaarkaart hebben volgemaakt, verzilveren ze die en stoppen ze het geld in een spaarrekening. Aan het einde van het jaar hebben ze €62,52 bespaard.
2. Het gezin spaart koopzegels dubbel via de Albert Heijn app. Daarmee kun je twee keer zo veel koopzegels kopen per euro aan producten. Aan het einde van het jaar bespaart het gezin hiermee €116,53 in totaal.
3. Het gezin kan besluiten naar een supermarkt te gaan die net iets goedkoper is, zoals de Jumbo of de Plus. Als hun kosten daarmee 2% verlagen, bespaart het gezin €218,99 bij elkaar.
4. Het gezin kan besluiten naar zogenaamde prijsvechters te gaan. Dit zijn supermarkten zoals de Aldi, Dirk of Lidl, die volgens een onderzoek in 2025 van Kassa ongeveer 15% goedkoper waren dan de Albert Heijn. Als ze het extra geld opsparen dat ze anders zouden hebben besteed bij de Albert Heijn, dan kunnen ze €1642,50 opzij zetten.

En deze getallen zijn nog gunstig, want een gezin van vier geeft relatief veel uit aan boodschappen! Als je koopzegels bekijkt voor een alleenstaande die 10 euro per dag uitgeeft bij de supermarkt, dan hebben de zegels na een jaar nauwelijks effect:

1. Koopzegels besparen de alleenstaande €17,53 per jaar.
2. Dubbele koopzegels besparen de alleenstaande €20,53 per jaar.
3. Een iets goedkopere supermarkt (2 procent goedkoper) levert de alleenstaande €62,41 per jaar op.
4. Een prijsvechtersupermarkt bezoeken i.p.v. een dure supermarkt kan €468,11 besparen per jaar.

Hoe meer je uitgeeft, des te beter de koopzegels

Je merkt heel erg dat koopzegels beter worden als je meer geld uitgeeft bij de supermarkt. En dat weet een supermarkt zoals de Albert Heijn. Als alleenstaande bespaar je een kleine 20 euro aan het einde van het jaar, maar dan moet je wel ongevoelig zijn voor de marketing van de Albert Heijn:

1. Om je bonuskaart in de app te scannen, moet je navigeren langs de reclamefolders die je aanmoedigen om producten te kopen.
2. Je moet de verleiding weerstaan om niet nét wat meer te kopen voor een extra koopzegel.
3. Zelfs als je koopzegels spaart, is het voordeliger om naar een goedkopere supermarkt te gaan. Veel mensen kiezen desalniettemin dikwijls voor de supermarkt waar ze koopzegels sparen, omdat ze denken dat ze daar voordeliger uit zijn.

Het dubbel sparen van koopzegels bij de Albert Heijn is ook zeer verraderlijk. Je kunt dubbel sparen voor koopzegels als je een Albert Heijn Premium abonnement afsluit, wat een jaarlijks abonnement van €14,99 is.

Een goeie deal, zou je denken, want dat verdien je terug met je dubbele koopzegels. In werkelijkheid verdien je dat pas terug als je €2450,– per jaar uitgeeft bij de Albert Heijn, en pas vanaf het bedrag daarboven verdien je extra aan je dubbele koopzegels. Voor een gezin is dit een haalbaar bedrag, maar een alleenstaande zal het merendeel van hun boodschappen bij de Albert Heijn moeten doen om geen extra kosten te maken.

Conclusie

Koopzegels leveren een stuk minder geld op dan je zou denken. Zelfs als een andere supermarkt nét iets goedkoper is, bespaar je meer geld door daarnaartoe te gaan. De prijsvechters zoals Aldi, Dirk en Lidl zijn meestal veel goedkoper dan dat.

Tuurlijk, áls je altijd naar dezelfde supermarkt gaat, dan is het voordeliger om in die winkel mee te doen aan koopzegels. Maar bedenk dus dat de opbrengst gaat om een paar tientjes per jaar, en niet om de enorme bedragen die je bij de servicebalie ontvangt – want het grootste deel van dat geld hád je al op je bankrekening staan.

Zelfs als je koopzegels verzamelt, is het altijd voordeliger om naar een goedkopere supermarkt te gaan.

Als je dan toch koopzegels wilt sparen, onthoud deze regel. Zelfs voor een klein prijsverschil is het niet de moeite waard om naar de duurdere winkel met koopzegels te gaan.

#maths

---

Ouder Nederlandstalig bericht <<<

Ouder bericht <<<

The Carter-Leslie Doomsday Argument is a probabilistic argument that claims the expected lifetime of humanity is proportional to the number of humans that have existed so far. More specifically, the chance of being part of the first 1% of humans is only 1% – so there might be a 99% chance of humans going extinct before reaching 100 times the number of humans that have existed so far.

This article contains a simulation that provides a counter-argument to the Doomsday Argument by arguing that one's position in the list of existing humans is independent of the total number of people. I will soon write a second article in which I go a bit deeper into the philosophical theory that constructs this bizarre problem.

Bayesian lottery

The Doomsday Argument was first introduced to me by a similar question: suppose you're participating in a lottery. You don't know how many others participate, but you are told that there's a 50% chance that 10 people participate, and there's a 50% chance that 1 trillion people participate. If you draw lottery number 5, what does that tell you about how many people participate?

Both one's intuition and Bayesian statistics tell you that the likelihood heavily favours the option where only 10 people participate, as drawing a ticket under 11 is a marginal chance in a trillion ticket lottery. With the Doomsday Argument, however, this logic can draw an emotional reaction from people: people don't want this logic to make sense, as the Doomsday Argument sounds rather chilling: with the recent population boom we've made, it suggests that the apocalypse is very likely imminent in a few generations.

At first, I wasn't too interested in the problem: I dismissed it as 'Bayesian trickery' – my own term for abusing Bayes' theorem to support wild claims. For example, people have used it to argue that we live in a simulation, that we must build a murderous AI superintelligence to avoid extinction and that God exists because miracles occur. Such arguments have brought me a certain level of skepticism for outlandish claims relying on Bayesian statistics. My counter-argument might be flawed or be utterly nonsensical, but my gut feeling remains that the Doomsday Argument is a well-crafted example of Bayesian trickery that has remained untamed for several decades now.

Simulations

Personally, I am a fan of using numeric simulations to make converging approximations of probabilities, as they help gain insight into how chances work.

For example, to simulate the lottery problem, the following script can offer some insight:

import random

N = 1_000_000
a, b = 0

# Sample N times
for _ in range(N):
    if random.random() < 0.5:
        # The lottery has 10 participants
        a += 1 if random.randint(1, 10) == 5 else 0
    else:
        # The lottery has 1 trillion participants
        b += 1 if random.randint(1, int(1e12)) == 5 else 0

# When drawing 5, this number represents the fraction of times the lottery had 10 participants.
# This number should be near 1.
print(a / (a + b))

We can even calculate that this fraction should converge to $\frac{\frac{1}{10}}{\frac{1}{10} + \frac{1}{10^{12}}} \approx 1 – 10^{-11}$.

Nevertheless, with a similar simulation, I will demonstrate how this analogy does not go for the Doomsday Argument.

Bug world

Enter Bug World, a hypothetical planet in our galaxy that hosts a wide variety of bugs that have a peculiar species lifetime. We'll test whether being “early” in humanity means doom is near, and we'll do that by having only some bugs thrive on Bug World. This lets us ask: do early bugs have reason to believe their species will end soon? Let's simulate!

On Bug World, every species is destined to go extinct after 10 bugs or after 1000 bugs. (We could've said 1 trillion, but that's too intense to simulate on contemporary hardware.) All bugs reproduce asexually and immediately die when they give birth, so there's always exactly one bug of every species alive. The 10th bug has a 50 percent chance of dying without reproducing the 11th bug. If the 11th bug is born, however, the species is guaranteed to go extinct after 1000 bugs have been born.

Since we're going to run this simulation on many species, we'll call a species a mayfly type if it goes extinct after the 10th bug, and we'll call it a millipede if the species survives until its 1000th bug. We'll call a bug young if it is one of the first 10 bugs in its species, and we'll call a millipede old if it is the 11th or latter specimen.

I have started a simulation. About every tick or so, a new bug species emerges in the world. At first, you notice a linear growth of new bugs, but the Bug World population stabilizes after the first millipedes start to go extinct. From there, the simulation mostly has a uniform distribution of all the bugs and their potential lifetimes.

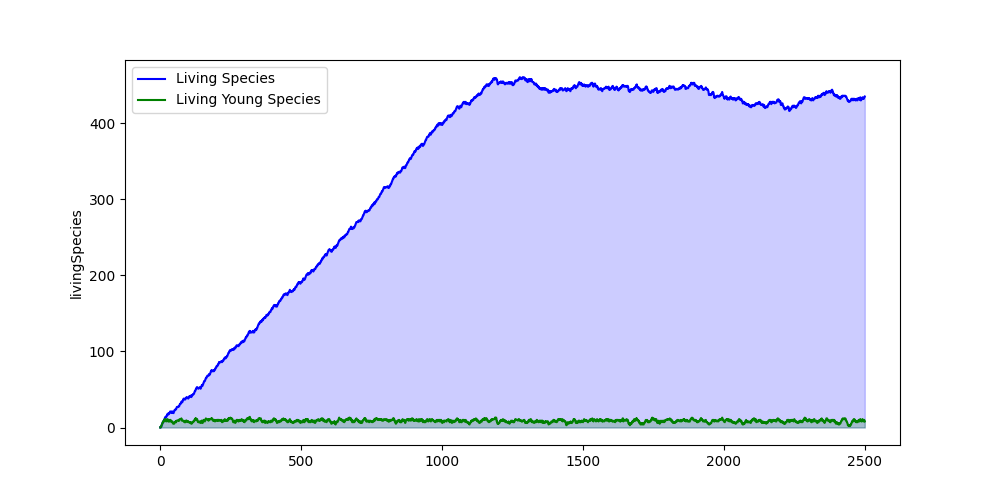
The graph shows in blue how many bugs are alive at a time step. The green line below shows how many of those bugs are still young. For those bugs, it isn't determined yet whether they are mayflies or millipedes.

Let's sample some bugs! Bug World simulates species that may end early (like humanity might). Sampling bugs is like asking: “Am I, a humble bug, early in my species’ timeline?” If the answer is yes, we'll move forward in time to see when the species goes extinct.

When sampling bugs from Bug World, I got the following results:

We sampled 10000 bugs, of which 208 (~2%) were young bugs.

Old millipede: 9792
Old mayfly: 0
Young species ended up being a millipede: 107
Young species ended up being a mayfly: 101
======================================
Odds of a millipede species dying old: 100%
Odds of selecting a young bug when sampling a millipede: ~1%
Odds of selecting a millipede when sampling a young bug: ~51%

These results indicate an interesting revelation! We sampled 10K bugs, and we can translate the Doomsday Argument to this situation: instead of wondering our own human position, let's look at the position of all young bugs. When sampling a young bug, there's a 50% chance of selecting a millipede or mayfly – despite the odds of selecting a young millipede being minimal! This means that a young bug cannot conclude it is likely a mayfly because it is a young bug.

Why is this result different from the simplified lottery example? I believe that the flaw in the Doomsday Argument is that it believes that you, the observer, are guaranteed to exist in any case of the Doomsday Argument. However, for the bugs on Bug World, 99% of the millipedes wouldn't exist if their species had been a mayfly.

Fire Lottery

Let's reshape the lottery thought experiment in a way where it demonstrates how I think the Doomsday Argument should be imagined. For this new lottery, there's 1 trillion people willing to participate. However, there has been a fire at the lottery factory, so not every participant receives a lottery ticket! You do, however, and you receive ticket number 5.

To me, the lottery represents being born, and the ticket represents your number in human history. The unique part about the fire lottery, however, is that you do not know the total number of lottery tickets remaining.

You can try reasoning that it's unlikely that you ended up in the bottom 1% of tickets and therefore there's a 99% chance of at most 500 tickets having been printed, but that clearly doesn't work. It's easy to see that you're overlooking the massive chance that you wouldn't have received a lottery ticket anyway.

I believe that these lottery tickets represent human existence in our world. This explains why the odds don't shift for young bugs in Bug World, and it shows the independence between the total number of humans to exist and the number of humans that have existed so far.

Conclusion

The Doomsday Argument assumes that your position among humans is informative about how many humans there will be. But both Bug World and the Fire Lottery suggest otherwise: if your existence depends on many people existing in the first place, then being “early” says little about the total number. In other words, your ticket number only matters if you were guaranteed a ticket in the first place.

The concept of Bug World touches on underlying concepts that I will touch on in a future article. I'll post a link here when that topic is there, or you can click on any of the hashtags to view all posts on a given topic.

#bayesian #doomsdayargument #maths #philosophy

---

Older English post <<< >>> Newer English post

Older post <<< >>> Newer post